This dataset was created by Prof. Bobak Nazer and Undergraduate Teaching Fellow Michael Clifford in 2018 for EK381. It consists of 1000 cat and 1000 dog images, each as a 64 x 64 grayscale image.
First was to simply classify cats and dogs using the simplest average classifier.
# Import Necessary Modules
import glob
import matplotlib.pyplot as plt
from skimage import io
import numpy as np
import math#This function reads in all images in catsfolder/ and dogsfolder/.
#Each 64 x 64 image is reshaped into a length-4096 row vector.
#These row vectors are stacked on top of one another to get two data
#matrices, each with 4096 columns. The first matrix cats consists of all
#the cat images as row vectors and the second matrix dogs consists of all
#the dog images as row vectors.
def read_cats_dogs():
# get image filenames
cat_locs = glob.glob('catsfolder/*.jpg')
dog_locs = glob.glob('dogsfolder/*.jpg')
num_cats = len(cat_locs)
num_dogs = len(dog_locs)
# initialize empty arrays
cats = np.zeros((num_cats,64*64))
dogs = np.zeros((num_dogs,64*64))
#reshape images into row vectors and stack into a matrix
for i in range(num_cats):
img = cat_locs[i]
im = io.imread(img)
im = im.reshape(64*64)
cats[i,:] = im
for i in range(num_dogs):
img = dog_locs[i]
im = io.imread(img)
im = im.reshape(64*64)
dogs[i,:] = im
return cats, dogs#Split dataset into training and test data.
cats_train = cats[0:math.floor(num_cats/2),:]
cats_test = cats[math.floor(num_cats/2):num_cats,:]
dogs_train = dogs[0:math.floor(num_dogs/2),:]
dogs_test = dogs[math.floor(num_dogs/2):num_dogs,:]
num_cats_test = cats_test.shape[0]
num_dogs_test = dogs_test.shape[0]#This function takes in a data matrix and outputs the
#average row vector.
def vector_average(datamatrix):
row_avg = np.mean(datamatrix, axis=0)
row_avg = row_avg.reshape(1, 4096)
print(row_avg.shape)
#Your code should go above this line.
if (row_avg.shape[0]!=1):
raise Exception("The variable avg_row is not a row vector.")
elif (row_avg.shape[1]!=datamatrix.shape[1]):
raise Exception("The variable row_avg does not have the same number of columns as the data matrix input.")
return row_avg#Calculate average cat and dogs images on the training data.
avg_cat = vector_average(cats_train)
avg_dog = vector_average(dogs_train)
show_image(avg_cat,0)
plt.title('Average Cat')
show_image(avg_dog,0)
plt.title('Average Dog')
#This function takes in a pet image currentpet (as a row vector) and
#two additional row vectors, avg_cat and avg_dog, corresponding to
#the average cat and dog images.
#The function should output 0 as its guess if currentpet is closer to
#avg_cat than avg_dog, and 1 as its guess if currentpet is closer to
#avg_dog than avg_cat. In the case of a tie, it should guess 1.
def hw3_classifier(currentpet,avg_cat,avg_dog):
difference_cat = np.subtract(avg_cat, currentpet)
difference_dog = np.subtract(avg_dog, currentpet)
abs_difference_cat = np.absolute(difference_cat)
abs_difference_dog = np.absolute(difference_dog)
sum_cat = np.sum(abs_difference_cat)
sum_dog = np.sum(abs_difference_dog)
if (sum_cat > sum_dog):
guess = 1
elif (sum_dog > sum_cat):
guess = 0
else:
guess = 1
#Your code should go above this line.
if ((guess!=0) & (guess!=1)):
raise Exception("The variable guess is not 0 or 1.")
return guess
#Classify test images.
cat_test_guesses = np.zeros((num_cats_test,1))
dog_test_guesses = np.zeros((num_dogs_test,1))
for i in range(num_cats_test):
current_cat = cats_test[i,:]
cat_test_guesses[i] = hw3_classifier(current_cat,avg_cat,avg_dog)
for i in range(num_dogs_test):
current_dog = dogs_test[i,:]
dog_test_guesses[i] = hw3_classifier(current_dog,avg_cat,avg_dog)def hw3_error_rate(cats_test_guesses,dogs_test_guesses):
cat_count = 0
dog_count = 0
print(len(cats_test_guesses))
for i in range(len(cats_test_guesses)):
if (cat_test_guesses[i] == 1):
cat_count += 1
for i in range(len(dogs_test_guesses)):
if (dogs_test_guesses[i] == 0):
dog_count += 1
cat_error_rate = cat_count/500
dog_error_rate = dog_count/500
#Your code should go above this line.
if ((cat_error_rate < 0) | (cat_error_rate > 1)):
raise Exception("The variable cat_error_rate is not between 0 and 1.")
elif ((dog_error_rate < 0) | (dog_error_rate > 1)):
raise Exception("The variable dog_error_rate is not between 0 and 1.")
return cat_error_rate, dog_error_rateThe project explores the classification of images, specifically focusing on handwriting samples, and distinguishing between cats and dogs. A key part of the analysis involves dimensionality reduction techniques, particularly Principal Component Analysis (PCA), to simplify the data while retaining critical information. This approach is crucial for improving classification performance and understanding the underlying structure of the data.
The dimensionality reduction techniques were applied to three different datasets:
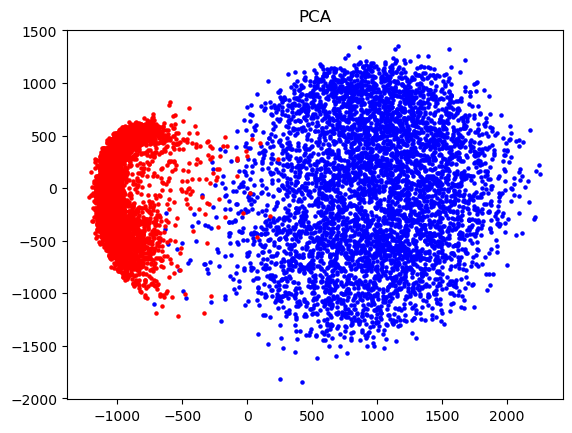
PCA being applied to the three datasets:


The handwriting dataset, upon visualization, appears more straightforward to classify compared to the benign and malignant datasets. This observation suggests a clear distinction between different classes (e.g., zeros and ones) that can be visually discerned.
The cats and dogs dataset presents a more challenging classification problem, with PCA revealing significant overlap between the two classes. This overlap indicates a less distinct separation, making the task of accurately distinguishing between cats and dogs more complex.
This project focuses on the development and application of a Linear Least Squares Estimation (LLSE) model to predict the compressive strength of concrete, a critical parameter in civil engineering and construction industries. Utilizing a dataset containing various mix design parameters of concrete, the project aims to establish a reliable predictive model that enhances our understanding of the factors influencing concrete's compressive strength.
This dataset came from the Concrete Compressive Strength Data Set created by I.-C. Yeh (initially for the paper [1]) and hosted by the UCI Machine Learning Repository [2].
The core of the project was the implementation of the LLSE method to estimate the compressive strength of concrete based on its mix design parameters. The model's performance was evaluated using Mean Squared Error (MSE) and the Coefficient of Determination (R²), providing insights into its predictive accuracy and reliability.
Through iterative testing, the model identified the mix design parameter with the highest predictive power for compressive strength. Additionally, the model was extended to include quadratic terms of the mix design parameters, aiming to capture non-linear relationships and improve predictive capability.
The project utilized scatter plots to visually compare actual vs. predicted values of concrete strength, facilitating an intuitive understanding of the model's performance. Both linear and quadratic models were evaluated to determine their effectiveness in predicting concrete strength.
This project focuses on the application of Linear Discriminant Analysis (LDA) and Quadratic Discriminant Analysis (QDA) for the classification of images into two categories: cats and dogs. Utilizing a dataset comprising grayscale images of cats and dogs, the project aims to develop and evaluate models that can accurately classify these images. The primary focus is on understanding how dimensionality reduction impacts the performance of LDA and QDA models in image classification tasks.
Principal Component Analysis (PCA) was employed to reduce the dimensionality of the image data, with experiments conducted over various dimensions (k-values) to assess the impact on model performance. LDA and QDA models were trained on the dimensionality-reduced data, with the dataset split into training and testing sets to evaluate model performance. Error rates were computed for both training and testing phases to assess the effectiveness of each model.
The project employed k-fold cross-validation to ensure robust evaluation of the models. This approach helped in understanding the generalization ability of the LDA and QDA models across different subsets of the data.
The project utilized scatter plots to visually compare actual vs. predicted values of concrete strength, facilitating an intuitive understanding of the model's performance. Both linear and quadratic models were evaluated to determine their effectiveness in predicting concrete strength.
Error rates for both LDA and QDA models were plotted against the number of dimensions used in PCA, revealing insights into the trade-offs between model complexity and overfitting.

